kepotimes.com – Simpangan baku dalam statistik, biasanya dilambangkan dengan σ , adalah ukuran variasi atau dispersi (mengacu pada tingkat peregangan atau pemerasan distribusi) di antara nilai-nilai dalam satu set data.
Semakin rendah standar deviasi, semakin dekat titik data cenderung ke mean (atau nilai yang diharapkan), μ.
Sebaliknya, deviasi standar yang lebih tinggi menunjukkan rentang nilai yang lebih luas.
Mirip dengan konsep matematika dan statistik lainnya, ada banyak situasi berbeda di mana standar deviasi dapat digunakan, dan dengan demikian banyak persamaan yang berbeda.
Selain untuk menyatakan variabilitas populasi, standar deviasi juga sering digunakan untuk mengukur hasil statistik seperti margin of error.
Jika digunakan dengan cara ini, deviasi standar sering disebut kesalahan standar dari mean, atau kesalahan standar perkiraan yang berkaitan dengan mean.
Kalkulator di atas menghitung deviasi standar populasi dan deviasi standar sampel, serta perkiraan interval kepercayaan.
Simpangan Baku untuk Populasi
Simpangan baku populasi, definisi standar σ , digunakan ketika seluruh populasi dapat diukur, dan merupakan akar kuadrat dari varian dari kumpulan data tertentu.
Dalam kasus di mana setiap anggota populasi dapat dijadikan sampel, persamaan berikut dapat digunakan untuk menemukan simpangan baku dari seluruh populasi:
- x i : adalah nilai individu
- μ : adalah rata-rata / nilai yang diharapkan
- N : adalah jumlah total nilai
Bagi mereka yang tidak terbiasa dengan notasi penjumlahan, persamaan di atas mungkin tampak menakutkan, tetapi ketika ditangani melalui komponen individualnya, penjumlahan ini tidak terlalu rumit.
Angka i = 1 dalam penjumlahan menunjukkan indeks awal, yaitu untuk kumpulan data 1, 3, 4, 7, 8, i = 1 akan menjadi 1, i = 2 akan menjadi 3, dan seterusnya.
Oleh karena itu, notasi penjumlahan berarti melakukan operasi (x i – μ 2 ) pada setiap nilai melalui N , yang dalam hal ini adalah 5 karena ada 5 nilai dalam kumpulan data ini.
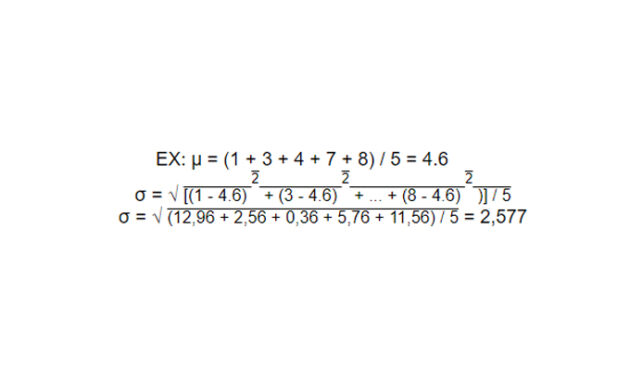
Contoh Simpangan Baku
Dalam banyak kasus, tidak mungkin untuk mengambil sampel setiap anggota dalam suatu populasi, yang mengharuskan persamaan di atas dimodifikasi sehingga deviasi standar dapat diukur melalui sampel acak dari populasi yang dipelajari.
Estimator umum untuk σ adalah simpangan baku sampel, biasanya dilambangkan dengan s .
Perlu dicatat bahwa terdapat banyak persamaan berbeda untuk menghitung simpangan baku sampel karena tidak seperti rata-rata sampel, simpangan baku sampel tidak memiliki penduga tunggal yang tidak bias, efisien, dan memiliki kemungkinan maksimum.
Persamaan yang diberikan di bawah ini adalah “deviasi standar sampel yang dikoreksi”.
Ini adalah versi koreksi dari persamaan yang diperoleh dari modifikasi persamaan deviasi standar populasi dengan menggunakan ukuran sampel sebagai ukuran populasi, yang menghilangkan beberapa bias dalam persamaan.
Estimasi yang tidak memihak dari deviasi standar bagaimanapun, sangat terlibat dan bervariasi tergantung pada distribusinya.
Dengan demikian, “deviasi standar sampel yang dikoreksi” adalah penduga yang paling umum digunakan untuk deviasi standar populasi, dan secara umum disebut hanya sebagai “deviasi standar sampel”.
Ini adalah perkiraan yang jauh lebih baik daripada versi yang tidak dikoreksi, tetapi masih memiliki bias yang signifikan untuk ukuran sampel yang kecil (N <10).
- x i : adalah satu nilai sampel
- x̄ : adalah rata-rata sampel
- N : adalah ukuran sampel
Lihat bagian “Simpangan Standar Populasi” untuk contoh bagaimana bekerja dengan penjumlahan.
Persamaannya pada dasarnya sama kecuali istilah N-1 dalam persamaan deviasi sampel yang dikoreksi, dan penggunaan nilai sampel.
Penerapan Standar Deviasi
Deviasi standar banyak digunakan dalam pengaturan eksperimental dan industri untuk menguji model terhadap data dunia nyata. Contoh dari ini dalam aplikasi industri adalah kontrol kualitas untuk beberapa produk.
Simpangan baku dapat digunakan untuk menghitung nilai minimum dan maksimum di mana beberapa aspek produk harus memiliki persentase waktu yang tinggi. Dalam kasus di mana nilai berada di luar kisaran yang dihitung, mungkin perlu dilakukan perubahan pada proses produksi untuk memastikan kendali mutu.
Simpangan baku juga digunakan dalam cuaca untuk menentukan perbedaan iklim regional.
Bayangkan dua kota, satu di pesisir dan satu lagi di pedalaman, yang memiliki suhu rata-rata 75 ° F. Meskipun hal ini mungkin memicu keyakinan bahwa suhu di kedua kota ini hampir sama, kenyataannya dapat disamarkan jika hanya mean yang dialamatkan dan deviasi standar diabaikan.
Kota-kota pesisir cenderung memiliki suhu yang jauh lebih stabil karena regulasi oleh badan air yang besar, karena air memiliki kapasitas panas yang lebih tinggi daripada daratan; pada dasarnya,
hal ini membuat air jauh lebih tidak rentan terhadap perubahan suhu, dan daerah pesisir tetap lebih hangat di musim dingin, dan lebih dingin di musim panas karena jumlah energi yang dibutuhkan untuk mengubah suhu air. Karenanya,
Bidang lain di mana deviasi standar sebagian besar digunakan adalah keuangan, di mana ia sering digunakan untuk mengukur risiko terkait dalam fluktuasi harga beberapa aset atau portofolio aset.
Penggunaan deviasi standar dalam kasus ini memberikan perkiraan ketidakpastian pengembalian masa depan atas investasi tertentu.
Misalnya, dalam membandingkan saham A yang memiliki pengembalian rata-rata 7% dengan standar deviasi 10% terhadap saham B, yang memiliki pengembalian rata-rata yang sama tetapi deviasi standar 50%, saham pertama jelas merupakan pilihan yang lebih aman,
karena deviasi standar saham B secara signifikan lebih besar, untuk pengembalian yang sama persis. Ini tidak berarti bahwa saham A secara definitif merupakan pilihan investasi yang lebih baik dalam skenario ini, karena deviasi standar dapat mengubah rata-rata di kedua arah.
Ini hanya beberapa contoh bagaimana seseorang dapat menggunakan deviasi standar, tetapi masih banyak lagi yang ada. Secara umum, menghitung deviasi standar sangat berharga setiap kali diinginkan untuk mengetahui seberapa jauh nilai rata-rata suatu distribusi dapat dari mean.
Ahir Kata
Nah, jadi itulah pembahasan dari kami mengenai Simpangan baku atau Standar Deviasi yang telah kami jelaskan paa kesempatan kali ini.
Semoga artikel diatas dapat membantu penyelesaian atau memecahkan masalah yang sedang kamu hadapi. Selamat Belajar dan Terimakasih.
Artikel Lainnya: