Kepotimes – Bilangan Eksponen merupakan operasi matematika, ditulis sebagai sebuah n , yang melibatkan dasar sebuah dan eksponen n . Dalam kasus di mana n adalah bilangan bulat positif, eksponen berhubungan dengan perkalian berulang dari basis, n kali.
a n = a × a × … × a
n kali
Hitungan di atas menerima basis negatif, tetapi tidak menghitung bilangan imajiner. Ini juga tidak menerima pecahan, tetapi dapat digunakan untuk menghitung eksponen pecahan, selama eksponen dimasukkan dalam bentuk desimalnya.
Rumus dan aturan Bilangan eksponen dasar
Saat eksponen yang memiliki basis yang sama dikalikan, eksponen ditambahkan.
a n × a m = a (n + m)
EX: 2 2 × 2 4 = 4 × 16 = 64
2 2 × 2 4 = 2 (2 + 4) = 2 6 = 64
Jika eksponen negatif, tanda negatif dihilangkan dengan membalik basis dan menaikkannya menjadi eksponen positif.
Artikel Lainnya: Barisan dan Deret
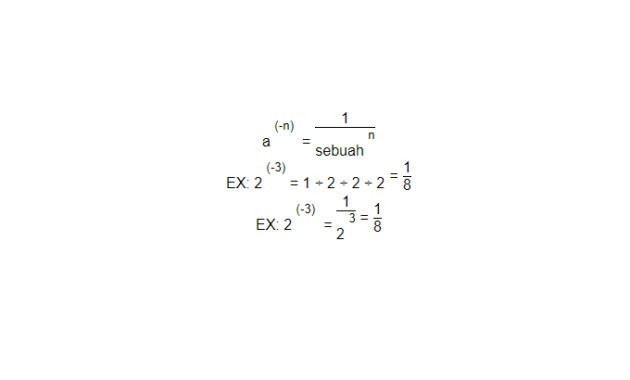
Saat eksponen yang memiliki basis yang sama dibagi, eksponen dikurangi.
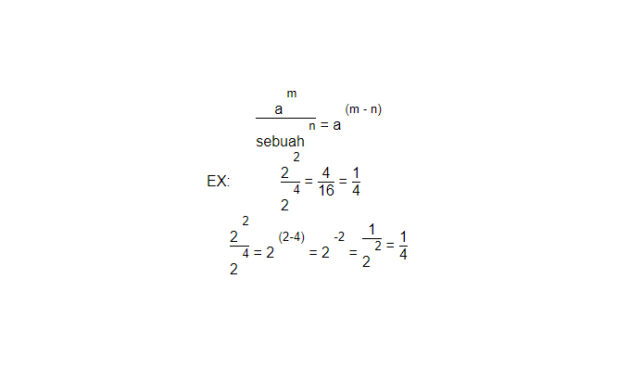
Ketika eksponen dipangkatkan ke eksponen lain, eksponen dikalikan.
(a m ) n = a (m × n)
EX: (2 2 ) 4 = 4 4 = 256
(2 2 ) 4 = 2 (2 × 4) = 2 8 = 256
Ketika basis yang dikalikan dinaikkan menjadi eksponen, eksponen didistribusikan ke kedua basis.
(a × b) n = a n × b n
EX: (2 × 4) 2 = 8 2 = 64
(2 × 4) 2 = 2 2 × 4 2 = 4 × 16 = 64
Demikian pula, ketika basis yang dibagi dinaikkan menjadi eksponen, eksponen didistribusikan ke kedua basis.

Jika eksponennya 1, basisnya tetap sama.
a 1 = a
Jika eksponen adalah 0, hasil eksponen basa apa pun akan selalu 1, meskipun beberapa perdebatan seputar 0 0 menjadi 1 atau tidak terdefinisi. Untuk banyak aplikasi, mudah mendefinisikan 0 0 sebagai 1.
a 0 = 1
Di bawah ini adalah contoh argumen untuk 0 = 1 menggunakan salah satu hukum eksponen yang disebutkan sebelumnya.
Jika a n × a m = a (n + m)
Maka a n × a 0 = a (n + 0) = a n
Jadi, satu-satunya cara untuk a n tetap tidak berubah dengan perkalian, dan hukum eksponen ini tetap benar, adalah untuk 0 menjadi 1.
Ketika eksponen adalah pecahan dengan pembilangnya 1, akar ke n dari basis diambil. Di bawah ini adalah contoh dengan eksponen pecahan di mana pembilangnya bukan 1.
Ia menggunakan kedua aturan yang ditampilkan, serta aturan untuk mengalikan eksponen dengan basis serupa yang dibahas di atas. Perhatikan bahwa kalkulator dapat menghitung eksponen pecahan, tetapi eksponen tersebut harus dimasukkan ke dalam kalkulator dalam bentuk desimal.
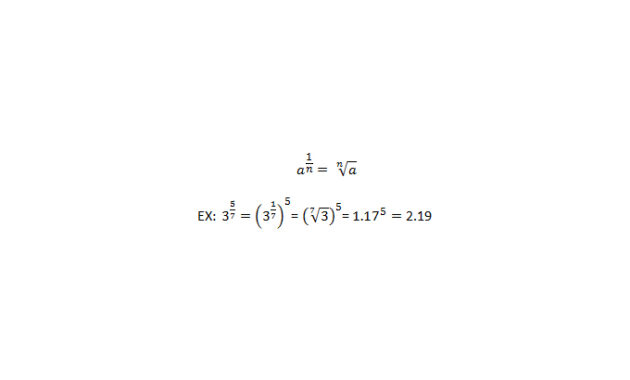
Artikel Lainnya:
Nah, jadi itulah pembahasan dari kami untuk mengenai materi Bilangan Eksponen yang telah kami ulas pada artikel kali ini.
Semoga artikel ini dapat menjadi referensi belajar kita untuk mengerjakan soal ataupun lainnya. Terimakasih