jurnalterakreditasi – Aljabar Matematika merupakan salah satu cabang tertua dalam sejarah matematika yang berhubungan dengan teori bilangan, geometri, dan analisis. Definisi aljabar terkadang menyatakan bahwa studi tentang simbol – simbol matematika dan aturan-aturannya, dan ini melibatkan manipulasi simbol-simbol matematika tersebut.

Aljabar mencakup hampir semua hal mulai dari menyelesaikan persamaan dasar hingga mempelajari abstraksi. Persamaan aljabar termasuk dalam banyak bab Matematika, yang akan dipelajari siswa di bidang akademik mereka. Juga, ada beberapa rumus dan identitas yang ada dalam aljabar.

Apa itu Aljabar Matematika?

Aljabar membantu memecahkan persamaan matematika dan membantu mendapatkan jumlah yang tidak diketahui, seperti bunga bank, proporsi, persentase. Variabel-variabel dalam aljabar dapat digunakan untuk merepresentasikan besaran-besaran yang tidak diketahui yang digabungkan sedemikian rupa untuk menulis ulang persamaan tersebut.

Rumus aljabar digunakan dalam kehidupan kita sehari-hari untuk mencari jarak, volume kontainer, dan untuk mengetahui harga jual jika diperlukan. Aljabar sangat membantu dalam menyatakan persamaan dan hubungan matematika dengan memanfaatkan huruf atau simbol lain yang mewakili entitas.

Kuantitas yang tidak diketahui dalam persamaan dapat diselesaikan melalui aljabar. Beberapa topik utama yang termasuk dalam aljabar termasuk Dasar-dasar aljabar, eksponen, penyederhanaan ekspresi aljabar, polinomial, persamaan kuadrat, dll.

Cabang Aljabar

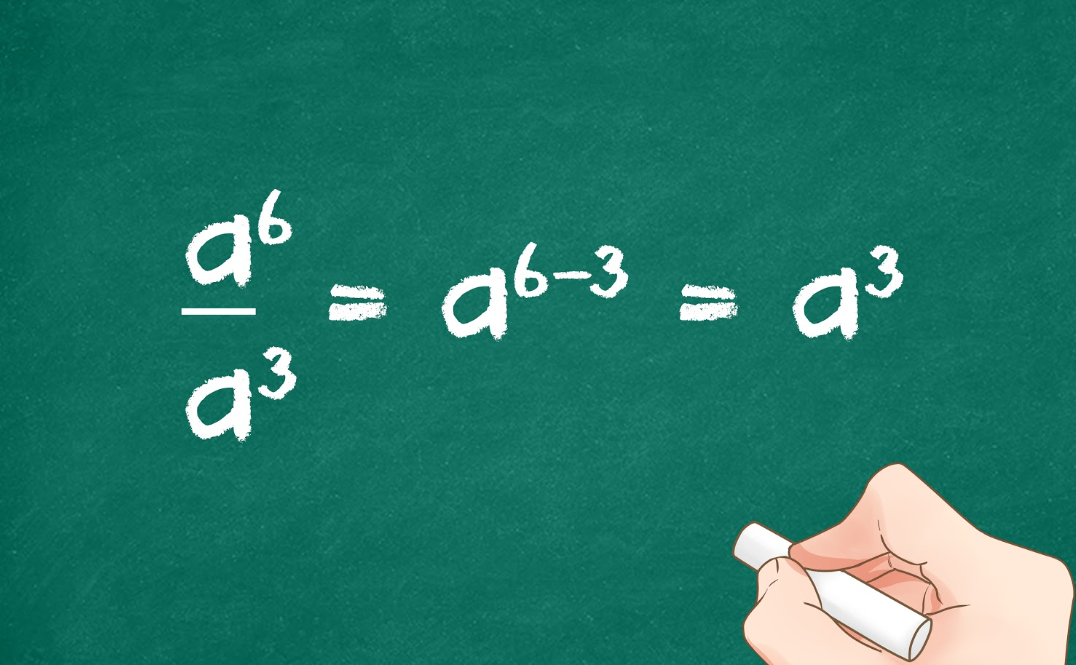
Artikel Lainnya: Penyajian Data dalam Diagram

Sebagaimana diketahui bahwa, aljabar merupakan konsep yang didasarkan pada nilai-nilai yang tidak diketahui yang disebut variabel. Konsep penting aljabar adalah persamaan. Ini mengikuti berbagai aturan untuk melakukan operasi aritmatika. Aturan digunakan untuk memahami kumpulan data yang melibatkan dua variabel atau lebih.

Ini digunakan untuk menganalisis banyak hal di sekitar kita. Anda mungkin akan menggunakan konsep aljabar tanpa menyadarinya. Aljabar dibagi menjadi beberapa sub cabang yang berbeda seperti aljabar dasar, aljabar lanjutan, aljabar abstrak, aljabar linier, dan aljabar komutatif.

Aljabar 1 atau Aljabar Dasar

Aljabar Dasar mencakup topik-topik tradisional yang dipelajari dalam kursus aljabar dasar modern. Aritmatika mencakup angka-angka bersama dengan operasi matematika seperti +, -, x, ÷. Namun dalam bidang aljabar, angka-angka tersebut seringkali diwakili oleh simbol-simbol dan disebut variabel seperti x, a, n, y.

Ini juga memungkinkan perumusan umum hukum aritmatika seperti, a + b = b + a dan ini adalah langkah pertama yang menunjukkan eksplorasi sistematis dari semua properti sistem bilangan real.

Konsep-konsep yang termasuk dalam aljabar dasar meliputi variabel, mengevaluasi ekspresi dan persamaan, sifat persamaan dan pertidaksamaan, menyelesaikan persamaan aljabar dan persamaan linier yang memiliki satu atau dua variabel, dan seterusnya.

Aljabar 2 atau Aljabar Lanjutan

Ini adalah Aljabar tingkat menengah. Aljabar ini memiliki tingkat persamaan yang tinggi untuk diselesaikan dibandingkan dengan pra-aljabar.

Aljabar tingkat lanjut akan membantu Anda mempelajari bagian-bagian lain aljabar seperti:

Persamaan dengan pertidaksamaan
Matriks
Menyelesaikan sistem persamaan linier
Membuat grafik dari fungsi dan persamaan linier
Bagian berbentuk kerucut
Persamaan Polinomial
Fungsi Kuadrat dengan pertidaksamaan
Polinomial dan ekspresi dengan radikal
Urutan dan seri
Ekspresi rasional
Trigonometri
Matematika diskrit dan probabilitas

Aljabar Abstrak

Aljabar abstrak adalah salah satu divisi dalam aljabar yang menemukan kebenaran yang berkaitan dengan sistem aljabar yang tidak bergantung pada sifat tertentu dari beberapa operasi.

Operasi ini, dalam kasus tertentu, memiliki properti tertentu. Dengan demikian kita dapat menyimpulkan beberapa konsekuensi dari properti tersebut. Karenanya cabang matematika ini disebut aljabar abstrak.

Aljabar abstrak berhubungan dengan struktur aljabar seperti bidang, grup, modul, cincin, kisi, ruang vektor, dll.

Konsep aljabar abstrak di bawah ini:

Set – Set didefinisikan sebagai kumpulan objek yang ditentukan oleh beberapa properti khusus untuk satu set. Misalnya – Himpunan semua matriks 2 × 2, himpunan vektor dua dimensi yang ada di bidang dan bentuk grup hingga yang berbeda.
Operasi Biner – Ketika konsep penjumlahan dikonseptualisasikan, ini memberikan operasi biner. Konsep semua operasi biner tidak akan berarti tanpa himpunan.
Elemen Identitas – Angka 0 dan 1 dikonseptualisasikan untuk memberikan gagasan tentang elemen identitas untuk operasi tertentu. Di sini, 0 disebut elemen identitas untuk operasi penjumlahan, sedangkan 1 disebut elemen identitas untuk operasi perkalian.
Elemen Invers – Gagasan elemen Invers muncul dengan angka negatif. Sebagai tambahan, kita tulis “ -a” sebagai invers dari “a” dan untuk perkalian, bentuk inversnya ditulis dengan “a ^{-1 ″} .
Asosiatif – Ketika bilangan bulat ditambahkan, ada properti yang disebut asosiatif di mana pengelompokan bilangan yang ditambahkan tidak memengaruhi penjumlahan. Perhatikan sebuah contoh, (3 + 2) + 4 = 3 + (2 + 4)

Artikel Lainnya: Pengertian Bentuk Rumus Garis dan Sudut

Aljabar linier

Aljabar linier adalah cabang aljabar yang berlaku baik untuk matematika terapan maupun matematika murni. Ini berkaitan dengan pemetaan linier antara ruang vektor.

Ini juga berkaitan dengan studi tentang bidang dan garis. Ini adalah studi tentang himpunan persamaan linier dengan properti transformasi. Ini hampir digunakan di semua bidang Matematika.

Ini menyangkut persamaan linier untuk fungsi linier dengan representasi mereka dalam ruang vektor dan melalui matriks. Topik penting yang dibahas dalam aljabar linier adalah sebagai berikut:

Persamaan linear
Ruang Vektor
Hubungan
Matriks dan dekomposisi matriks
Relasi dan Perhitungan

Aljabar komutatif

Aljabar komutatif merupakan salah satu cabang dari aljabar yang mempelajari cincin komutatif dan cita-citanya.

Teori bilangan aljabar, serta geometri aljabar, bergantung pada aljabar komutatif. Ini mencakup cincin bilangan bulat aljabar, cincin polinomial, dan seterusnya.

Ada banyak bidang matematika lain yang memanfaatkan aljabar komutatif dengan cara yang berbeda seperti topologi diferensial, teori invarian, teori urutan, dan topologi umum. Ini telah menempati peran luar biasa dalam matematika murni modern.

Artikel Lainnya: Pengertian dan macam bentuk Aljabar

Nah, jadi itulah pembahasan dari kami mengenai materi Aljabar Matematika pada kesempatan kali ini. Semoga dengan artikel ini bisa membantu anda memahami tentang rumus matematika terlebih tentang Penyajian Data dalam Diagram, selamat belajar dan terima kasi