Dosen jurnalterakreditasi – Garis dan Sudut, Dalam geometri, garis adalah gambar yang terdiri dari titik tak hingga yang memanjang tanpa batas di kedua arah. Garis lurus dan memiliki kedalaman atau lebar yang dapat diabaikan.

Ada berbagai macam garis yang akan Anda pelajari, seperti garis tegak lurus, garis berpotongan, garis transversal, dll. Sudut adalah gambaran di mana dua sinar muncul dari titik yang sama.

Anda juga bisa menemukan sudut alternatif dan bersesuaian di bidang ini. Bentuk geometri dan propertinya adalah cabang matematika paling praktis. Sebagian besar konsep ini telah diajarkan di Kelas 7 dan Kelas 9. Mari kita kumpulkan lebih banyak informasi.

Garis dan Sudut – Definisi Dan Bagiannya

Di sini, mari kita bahas, definisi dasar dan sifat garis dan juga untuk sudut. Ini akan memberi siswa pengetahuan dasar tentang istilah-istilah geometris ini.

Garis pada dasarnya dikategorikan sebagai:

Segmen garis
sinar

Sudut pada dasarnya diklasifikasikan sebagai:

Sudut Akut (<90 °)
Sudut Kanan (= 90 °)
Sudut Obtuse (> 90 °)
Sudut Lurus (180 °)

Berdasarkan konsep atau operasi yang dilakukan pada baris, mereka adalah;

Garis sejajar
Garis Tegak Lurus
Lintang

Dan berdasarkan hubungan antara dua sudut, secara konseptual, mereka adalah;

Sudut Tambahan
Sudut Pelengkap
Sudut yang Berdekatan
Sudut Berlawanan Vertikal

Artikel Lainnya: Cara Menghitung Rumus Bola Dengan Mudah

Segmen garis

Segmen garis adalah bagian dari garis dengan dua titik akhir. Ini adalah jarak terpendek antara dua titik dan memiliki panjang tetap.

sinar

Sinar adalah bagian dari garis, yang memiliki titik awal dan memanjang tanpa batas ke satu arah.

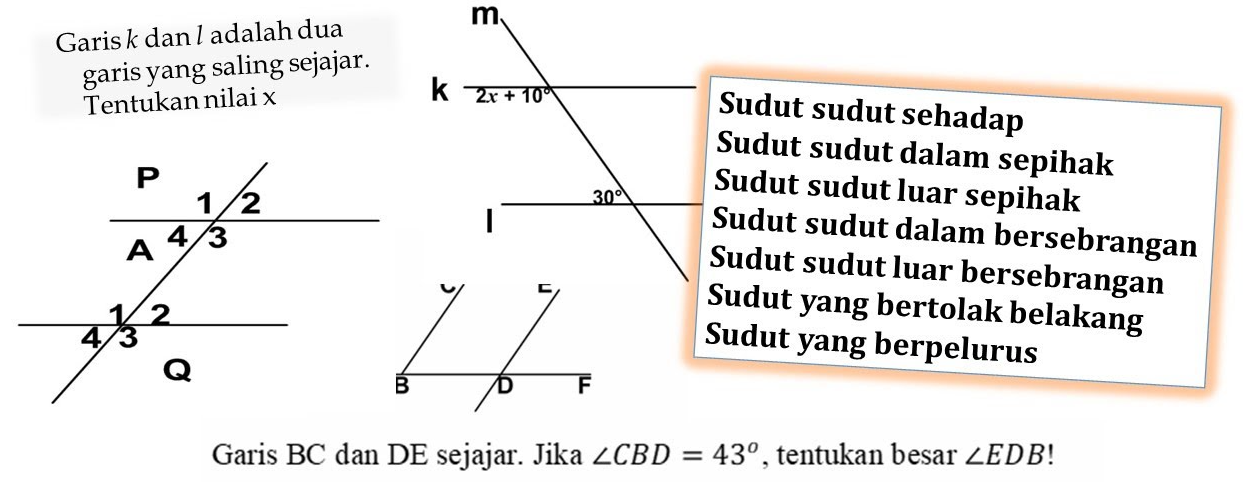
Garis Tegak Lurus

Ketika dua garis membentuk sudut siku-siku satu sama lain, dengan bertemu pada satu titik, disebut garis tegak lurus. Pada gambar, Anda bisa melihat, garis AB dan CD saling tegak lurus.

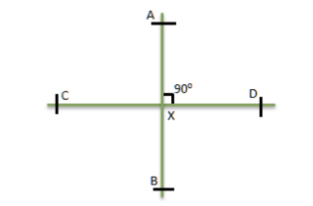
Garis sejajar

Dua garis dikatakan sejajar jika tidak bertemu di titik mana pun dalam bidang atau yang tidak saling berpotongan. Pada gambar, garis PQ dan RS sejajar satu sama lain.

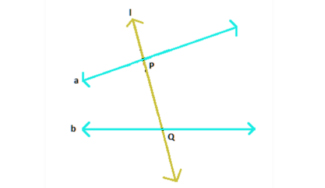
Garis Transversal

Ketika sebuah garis memotong dua garis pada titik yang berbeda, itu disebut transversal. Pada gambar, l transversal memotong dua garis pada titik P dan Q.

Properti Garis

Collinear point adalah sekumpulan tiga atau lebih titik yang terletak pada garis yang sama.
Titik-titik yang tidak terletak pada garis yang sama disebut titik-titik non-collinear.

Catatan: Tiga titik dapat berupa collinear atau non-collinear, tetapi tidak keduanya bersamaan pada saat yang bersamaan.

Artikel Lainnya:Rumus Lengkap MateriTeorema Pythagoras

Sudut lancip

Jika kemiringan di antara lengan kurang dari sudut siku-siku, itu disebut sudut lancip.

Sudut tumpul

Jika kemiringan antara lengan lebih dari sudut siku-siku, itu disebut sudut tumpul.

Sudut kanan

Jika lengan membentuk sudut 90 derajat di antara keduanya, itu disebut sudut siku-siku.

Sudut Lurus

Jika lengan membentuk sudut 180 derajat di antara keduanya, itu disebut sudut lurus.

Sudut Pelengkap

Dua sudut yang jumlahnya mencapai 90 derajat disebut sudut komplementer.

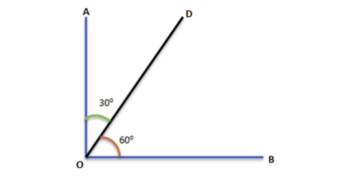
Sudut Tambahan

Dua sudut yang jumlahnya sampai 180 derajat disebut sudut tambahan.

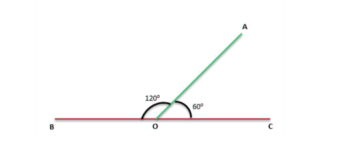
Sudut yang Berdekatan

Dua sudut yang memiliki sisi yang sama dan satu titik sudut yang sama disebut sudut yang berdekatan. Pada gambar berikut, ∠α dan ∠β adalah sudut yang berdekatan.

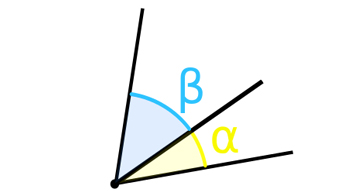
Sudut Berlawanan Vertikal

Dua sudut yang terbentuk, berlawanan satu sama lain, ketika dua garis berpotongan pada titik atau titik yang sama, disebut sudut yang berlawanan secara vertikal. Pada gambar, diberikan di bawah ini;

∠POR = ∠SOQ dan ∠POS = ∠ROQ

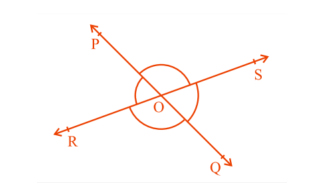
Bagian Sudut

Sudut adalah gambaran di mana dua sinar muncul dari titik yang sama. Titik ini disebut titik sudut dan dua sinar yang membentuk sudut disebut lengan atau sisi.
Sudut yang lebih besar dari 180 derajat tetapi kurang dari 360 derajat disebut sudut refleks.
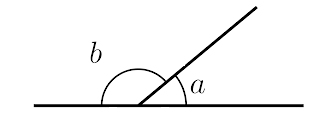
Jika dua sudut yang berdekatan berjumlah 180 derajat, mereka membentuk sepasang sudut linier. Pada gambar berikut, ∠a dan ∠b membentuk pasangan linier.

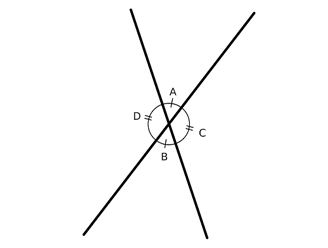
Ketika dua garis berpotongan satu sama lain, dua pasang sudut berlawanan yang terbentuk disebut sudut yang berlawanan secara vertikal. Pada gambar berikut, ∠A dan ∠B adalah sudut yang berlawanan secara vertikal. Pasangan lainnya adalah ∠C dan ∠D.

Artikel Lainnya: Jarimatika Penjumlahan dan Pengurangan

Nah, jadi itulah pembahasan dari kami mengenai materi Garis dan Sudut pada kesempatan kali ini.

semoga dengan artikel ini bisa membantu anda memahami tentang rumus matematika terlebih tentang koordinat kartesius, selamat belajar dan terima kasih.