jurnalterakreditasi – Dalam matematika, sistem koordinat Kartesius (atau sistem koordinat persegi panjang ) digunakan untuk menentukan setiap titik secara unik dalam sebuah bidang melalui dua bilangan , biasanya disebut koordinat x dan koordinat y titik.
Untuk menentukan koordinat, ditentukan dua garis tegak lurus ( sumbu x atau absis, dan sumbu y atau ordinat), serta panjang satuan, yang ditandai pada dua sumbu (lihat Gambar dibawah).
Sistem koordinat kartesius juga digunakan di ruang angkasa (di mana tiga koordinat digunakan) dan dalam dimensi yang lebih tinggi.
Dengan menggunakan sistem koordinat kartesius, bentuk geometris (seperti kurva ) dapat digambarkan dengan persamaan aljabar, yaitu persamaan yang dipenuhi oleh koordinat titik-titik yang terletak pada bentuk tersebut.
Misalnya, lingkaran dengan jari-jari 2 dapat dijelaskan dengan persamaan x² + y² = 4. Persamaan lingkaran tersebut adalah x² + y² = 4.
Sistem koordinat dua dimensi
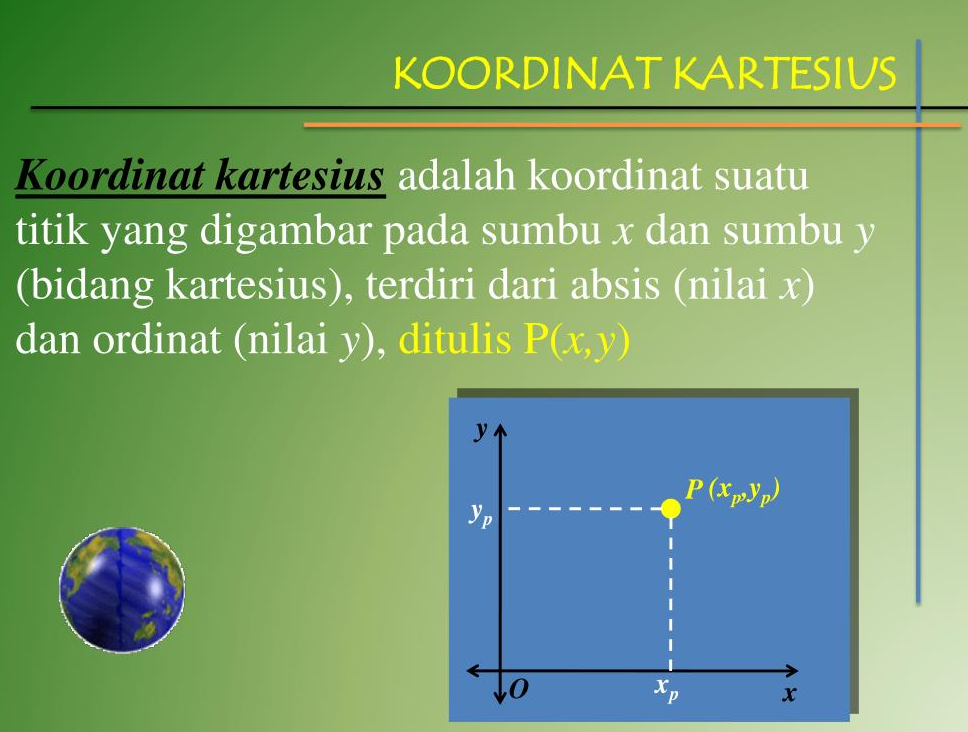
Sistem koordinat kartesius dalam dua dimensi umumnya ditentukan oleh dua sumbu, bersudut siku-siku satu sama lain, membentuk bidang (bidang xy ). Sumbu horizontal biasanya diberi label x , dan sumbu vertikal biasanya diberi label y .
Dalam sistem koordinat tiga dimensi, sumbu lain, biasanya diberi label z , ditambahkan, memberikan pengukuran ruang dimensi ketiga.
Artikel Lainnya: Cara Mengerjakan Soal Turunan Fungsi Dengan Mudah
Sumbu biasanya didefinisikan sebagai saling ortogonal satu sama lain (masing-masing pada sudut siku-siku).
(Sistem awal mengizinkan sumbu “miring”, yaitu sumbu yang tidak bertemu pada sudut siku-siku, dan sistem semacam itu kadang-kadang digunakan saat ini, meskipun sebagian besar sebagai latihan teoretis.)
Semua titik dalam sistem koordinat Kartesius diambil bersama-sama membentuk benda- dipanggil Pesawat Cartesian . Persamaan yang menggunakan sistem koordinat Kartesius disebut persamaan Kartesius .
Titik persimpangan, di mana sumbu bertemu, disebut asal biasanya berlabel O. The x dan y sumbu mendefinisikan sebuah pesawat yang disebut sebagai xy plane. Diberikan setiap sumbu, pilih panjang satuan, dan tandai setiap satuan di sepanjang sumbu, membentuk kisi.
Untuk menentukan titik tertentu pada sistem koordinat dua dimensi, tunjukkan unit x terlebih dahulu ( absis ), diikuti dengan unit y ( ordinat ) dalam bentuk ( x , y ), pasangan berurutan.
Pilihan huruf berasal dari konvensi, menggunakan bagian akhir alfabet untuk menunjukkan nilai yang tidak diketahui. Sebaliknya, bagian pertama alfabet digunakan untuk menunjukkan nilai yang diketahui.
Contoh titik P pada sistem ditunjukkan pada Gambar 3, menggunakan koordinat (3,5).
Perpotongan dua sumbu membentuk empat daerah, disebut kuadran , yang ditunjukkan dengan angka Romawi I (+, +), II (-, +), III (-, -), dan IV (+, -).
Secara konvensional, kuadran diberi label berlawanan arah jarum jam dimulai dari kuadran kanan atas (“timur laut”). Pada kuadran pertama, kedua koordinat bernilai positif, pada kuadran kedua koordinat x negatif dan koordinat y positif,
pada kuadran ketiga kedua koordinat bernilai negatif dan pada kuadran keempat koordinat x bernilai positif dan koordinat y negatif .
Artikel Lainnya: Lingkaran Matematika
Sistem koordinat tiga dimensi
Sistem koordinat Kartesius tiga dimensi menyediakan tiga dimensi fisik ruang — panjang, lebar, dan tinggi. Gambar 4 dan 5, menunjukkan dua cara umum untuk
merepresentasikannya.
Tiga sumbu Cartesian yang mendefinisikan sistem saling tegak lurus. Koordinat yang relevan adalah dalam bentuk (x, y, z) .
Sebagai contoh, gambar 4 menunjukkan dua titik yang diplot dalam sistem koordinat Kartesius tiga dimensi: P (3,0,5) dan Q (−5, −5,7).
Sumbu digambarkan dalam orientasi “koordinat dunia” dengan sumbu z mengarah ke atas.
The x -, y -, dan z -coordinates dari titik juga dapat diambil sebagai jarak dari yz -pesawat, xz -pesawat, dan xy -pesawat masing-masing. Gambar 5 menunjukkan jarak titik P dari bidang.
Pesawat xy -, yz -, dan xz membagi ruang tiga dimensi menjadi delapan subdivisi yang dikenal sebagai oktan, mirip dengan kuadran ruang 2D.
Meskipun konvensi telah ditetapkan untuk pelabelan empat kuadran bidang x – y , hanya oktan pertama dari ruang tiga dimensi yang diberi label. Ini berisi semua titik yang koordinat x , y , dan z -nya positif.
Artikel Lainnya: Rumus Turunan Fungsi dalam Matematika
Nah, jadi itulah pembahasan dari kami mengenai materi Koordinat kartesius pada kesempatan kali ini / Semoga dengan artikel ini bisa membantu anda memahami tentang rumus matematika terlebih tentang koordinat kartesius, selamat belajar dan terima kasih.