Materi Persamaan Kuadrat dan Jenis-Jenis Akar & Contoh Soal

by

kepotimes.com – Rumus matematika materi persamaan kuadrat – Persamaan kuadrat adalah persamaan polynomial berorde dua (berpangkat dua (2)) dengan bentuk umum y = ax2 + bx + c

dimana a tidak sama dengan 0 dan a merupakan koefisien dari x2, b koefisien dari x, dan c adalah konstanta (tidak mempunyai variabel). Persamaan kuadrat ini wajib kita pahami karena tidak hanya ada pada soal ujian sekolah saja,

namun selalu ada dalam soal tes perguruan tinggi (SBMPTN), jadi minimal kita harus memahami dasar-dasar nya terlebih dahulu.

Jenis-jenis Akar Persamaan Kuadrat

materi persamaan kuadrat

Persamaan kuadrat mempunyai beberapa jenis akar persamaan bergantung dengan nilai D atau diskriminan nya. Dimana D = b2 – 4ac dengan ketentuan sebagai berikut,

  1. D > 0, persamaan ax2 + bx + c = 0 mempunyai dua akar real yang berbeda
  2. D = 0, persamaan ax2 + bx + c = 0 mempunyai dua akar real kembar
  3. D < 0, persamaan ax2 + bx + c = 0 mempunyai dua akar imajiner

Materi Singkat Materi persamaan kuadrat. Untuk menyelesaikan soal persamaan kuadrat, kita harus dapat menentukan akar-akar nya atau nilai x.

Karena merupakan persamaan polynomial berorde dua, jadi nilai x atau akar-akar yang kita tentukan ada dua kemungkinan. Caranya bagaimana? Setidaknya ada tiga cara yang bisa digunakan yaitu dengan cara memfaktorkan, kuadrat sempurna,

dan menggunakan rumus ABC. Agar lebih paham, yuk kita langsung masuk ke contoh soal nya saja!

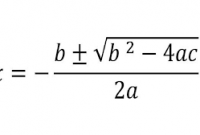
fungsi persamaan kuadrata

Contoh soal persamaan kuadrat

  1. Selesaikan dan tentukan jenis akar pada persamaan kuadrat x2 + 8x + 15 = 0 dengan menggunakan a) pemfaktoran, b) kuadrat sempurna, dan c) rumus ABC!

Pembahasan:

  1. Pemfaktoran

X2 + 8x + 15                                 = 0

(x + 3) (x + 5)              = 0

x + 3 = 0 atau x + 5 = 0

Sehingga x = -3 atau x = -5

Jadi HP (Himpunan Penyelesaian) = {–3, –5}

  1. Kuadrat Sempurna

X2 + 8x + 15                                 = 0

X2 + 8x                           = -15

X2 + 8x + 16                 = -15 + 16

(x + 4)2                                       = 1

X + 4                              = ± 1

X = 1 – 4 atau X = 1 + 4

Sehingga X = -3 atau X = -5

Jadi HP (Himpunan Penyelesaian) = {–3, –5}

  1. Rumus ABC

Sebelumnya, kita harus mengetahui rumus ABC dibawah ini,

X2 + 8x + 15                                 = 0

a = 1, b = 8, dan c = 15

X(1,2)            = –

X(1,2)            =

X = (-8 – 2)/2 atau X = (-8 + 2 )/2

Sehingga X = -5 atau X = -3

Jadi HP (Himpunan Penyelesaian) = {–3, –5}

  1. Jenis akar persamaan kuadrat x2 + 8x + 15 = 0

D     = b2 – 4ac

= 82 – 4(1)(15)

= 4

Jadi D > 4, sehingga dapat disimpulkan persamaan x2 + 8x + 15 = 0 mempunyai dua akar real yang berbeda

nah itulah pembahasan tentang materi persamaan kuadrat yang bisa anda ikuti beserta contoh soal sederhana yang bisa anda jadikan analogi ketika

menghadapi soal matematika tentang persamaan kuadrat, pertidaksamaan kuadrat dan lainya.

semoga dengan artikel ini bisa memberikan anda informasi yang berguna, jangan lupa kunjungi terus kepotimes.com untuk update rumus matematika setiap harinya agar anda semakin jago dalam matematika. selamat belajar dan terima kasih.

Artikel Lainnya: