jurnalterakreditasi – Teorema Pythagoras merupakan topik penting dalam Matematika yang menjelaskan hubungan antara sisi-sisi segitiga siku-siku. Kadang-kadang juga disebut Teorema Pythagoras. Rumus dan bukti teorema ini dijelaskan di sini dengan contoh-contoh.

Teorema ini pada dasarnya digunakan untuk segitiga siku-siku dan yang dengannya kita dapat menurunkan rumus alas, tegak lurus dan miring. Mari kita pelajari teorema ini secara rinci di sini.

Teorema Pythagoras

Teorema Pythagoras menyatakan bahwa ” Dalam segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat dari dua sisi lainnya “.

Sisi-sisi segitiga ini dinamai Tegak Lurus, Alas dan Sisi Miring. Di sini, sisi miring adalah sisi terpanjang, karena berlawanan dengan sudut 90 °.

Sisi-sisi segitiga siku-siku (katakanlah x, y dan z) yang memiliki nilai bilangan bulat positif, jika dikuadratkan, dimasukkan ke dalam persamaan, juga disebut rangkap tiga Pythagoras.

Rumus Teorema Pythagoras

Pertimbangkan segitiga yang diberikan di atas:

Di mana “a” adalah sisi tegak lurus,

“B” adalah dasarnya,

“C” adalah sisi miring.

Menurut definisi tersebut, rumus Teorema Pythagoras diberikan sebagai:

Miring ² = Tegak lurus ² + dasar ²c ² = a ² + b ²

Sisi yang berlawanan dengan sudut siku-siku (90 °) adalah sisi terpanjang (dikenal sebagai Sisi Miring) karena sisi yang berlawanan dengan sudut terbesar adalah yang terpanjang.

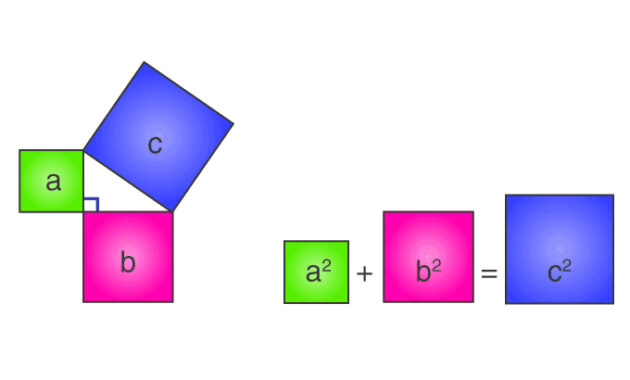
Pertimbangkan tiga kotak sisi a, b, c yang dipasang pada tiga sisi segitiga yang memiliki sisi yang sama seperti yang ditunjukkan.

Dengan Teorema Pythagoras –

Luas persegi A + Luas persegi B = Luas persegi C

Contoh

Contoh teorema berdasarkan pernyataan yang diberikan untuk segitiga siku-siku diberikan di bawah ini:

Pertimbangkan segitiga siku-siku, yang diberikan di bawah ini:

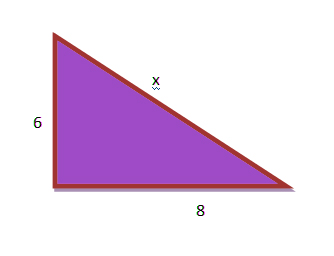
Temukan nilai x.

X adalah sisi yang berlawanan dengan sudut siku-siku, oleh karena itu X adalah sisi miring.

Sekarang, dengan teorema kita tahu;

Sisi Miring ² = Alas ² + Tegak Lurus ²

x ² = 8 ² + 6 ²

x ² = 64 + 36 = 100

x = √100 = 10

Artikel Lainnya: Rumus Lingkaran Matematika

Bukti Teorema Pythagoras

Diketahui: Segitiga siku-siku ABC, siku-siku di B.

Untuk Membuktikan- AC ² = AB ² + BC ²

Konstruksi: Gambarkan BD yang menyambung AC di D.

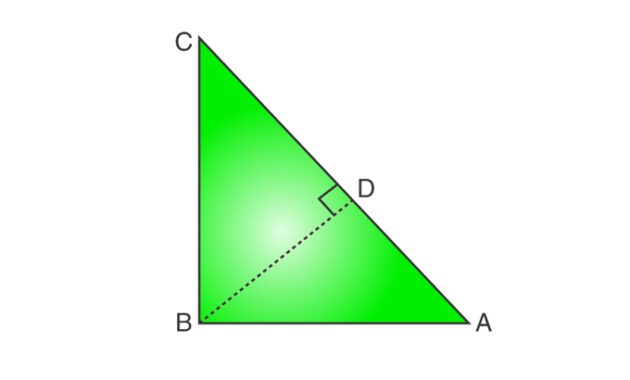
Bukti: Pertama, kita harus menjatuhkan BD yang tegak lurus ke sisi AC

Kami tahu, △ ADB ~ △ ABC

Karena itu, A DA B=A BA C (sisi yang sesuai dari segitiga serupa)

Atau, AB ² = AD × AC …………………………… .. …… .. (1)

Juga, △ BDC ~ △ ABC

Karena itu, CDB C=B CA C (sisi yang sesuai dari segitiga serupa)

Atau, BC ² = CD × AC …………………………………… .. (2)

Menambahkan persamaan (1) dan (2) kita dapatkan,

AB ² + BC ² = AD × AC + CD × AC

AB ² + BC ² = AC (AD + CD)

Karena, AD + CD = AC

Oleh karena itu, AC ² = AB ² + BC ²

Oleh karena itu, teorema Pythagoras terbukti.

Artikel Lainnya: Rumus Bilangan Eksponen

Penerapan Teorema Pythagoras

Untuk mengetahui apakah segitiga itu segitiga siku-siku atau bukan.
Dalam segitiga siku-siku, kita bisa menghitung panjang sisi mana pun jika kedua sisi lainnya diberikan.
Untuk mencari diagonal persegi.

Berguna untuk

Teorema Pythagoras berguna untuk mencari sisi dan sudut segitiga siku-siku. Jika kita mengetahui dua sisi segitiga siku-siku, maka kita bisa mencari sisi ketiganya.

Cara Penggunaan?

Untuk menggunakan teorema ini, ingat rumus yang diberikan di bawah ini:

c ² = a ² + b ²

Dimana a, b dan c adalah sisi-sisi segitiga siku-siku.

Misalnya, jika nilai a = 3 cm, b = 4 cm, maka carilah nilai c.

Kita tahu,

c ² = a ² + b ²

c ² = 3 ² +4 ²

c ² = 9 + 16

c ² = 25

c = √25

c = 5

Makanya, sisi ketiga adalah 5 cm.

Seperti yang bisa kita lihat, a + b> c

3 + 4> 5

7> 5

Oleh karena itu, c = 5 cm adalah sisi miring dari segitiga tersebut.

Artikel Lainnya: Pengertian dan Rumus Barisan dan Deret

Nah, jadi itulah pembahasan dari kami untuk mengenai materi Lingkaran Matematika yang telah kami ulas pada artikel kali ini.

Semoga artikel ini dapat menjadi referensi belajar kita untuk mengerjakan soal ataupun lainnya. Terimakasih